justplay

还是发博客叭

素性检测实验报告

1. 算法实现

1.1 sage实现

1.1.1 单轮素性检测

from random import *

def Fermat(p):
    a=randint(2,p-1)
    return  pow(a,p-1,p)==1

def Solovay_Strassen(p):
    a=randint(2,p-1)
    t=pow(a,(p-1)//2,p)
    return t==jacobi_symbol(a,p)


def Miller_rabin(n):
    b=randint(1,n-1)
    if n == 2 or n == 3:
        return True

    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    x = pow(b, s, n)
    if x == 1 or x == n - 1:
        continue
    for _ in range(r - 1):
        x = pow(x, 2, n)
        if x == n - 1:
            break
    else:
        return False
    return True

需要注意的是，在sage中集成了jacobi符号，函数名为jacobi_symbol,输入为a,b,其中b为正奇数，a为整数，输出为-1，0，1，所以我们直接使用了集成函数以声明来源。而事实上，在经典实现中，本段其实应该用t==1 or t==-1 代替。(ps.用sage跑，得到的pow是在环上的，这时==是同余，用python跑请用p-1代替-1)

那么，为何不用判断t是否为0呢？这样做除了效率因素外又是否有其他考究？

下面我们将从两个方面进行说明。

从素性检测的角度，我们知道，jacobi符号是对legendre符号denominator非素时的推广，其为-1或1，而推广中0的结果是由于合数的归约所导致，所以当jacobi_symbol==0时，其本身就代表了对待测数素数性的一个推翻，故不能加入判断。
从模幂运算的角度，我们知道，一个非0数在有限域上的幂必然不为0。在实数域上这是显然的，但在其他数环中未必成立，我们不妨从GF(p)有限域开始来证明一下。

我们假设，在有限域GF(p)中存在数a，b，使得\[a^b \equiv 0 \pmod {p}\],则有\[a^b|p\],而已知由于有限域，p为素数只有一个素因子，即其本身p，在\[GF(p)\]中，对于任意a，\[a\not{|} \space p\],所以与上式矛盾，因此此时不存在这样的数a满足pow(a,b,p)==0

同理拓展，对于任意整数m进行唯一素分解,即\[m=p^{n_1}_1 p^{n_2}_2 p^{n_3}_3\cdots\],当\[n_i\]均为1时，对于任意a，均存在\[p_i\],有\[a\not {|}\space p _i\]，进而原式可被规约至\[GF(p_i)\]上，可知其也不存在pow(a,b,m)==0的情况。

而当\[\exist n_i\neq 1\]时，则将存在\[m_1=p_1 p_2 p_3\cdots\]，这时必有\[n_{max}=max(n_i)\]，使得\[m_1^{n_{max}}|m\]，即\[pow(m_1,n_{max},m)==0\]，不过这时如素性检测所言也是不合法的情况。

在这里写下这些其实是为了说明一个问题，对于素数，我们可以发现素性检测必然成立，但是对于一些具有特殊性质的合数，在某些检验的方面他们并不如同质数与合数的划分那么清晰(如对于模幂运算后是否可能为0这个我们上文自己提出的划分标准就有可列举的反例，若加入判断则会有含有质数幂方的因子的数失效)，一些数字依然会在某些检测中被略过——这也是我写下这篇博客的缘由，所以我们需要进行多轮素性检测以增加准确性。

1.1.2 多轮素性检测

def fermat(p,b):
	for i in range(b):
		if not Fermat(p):
			return False
	return True	

def solovay_Strassen(p,b):
	for i in range(b):
		if not Solovay_Strassen(p):
			return False
	return True


def miller_rabin(n, b):
    """
    Miller Rabin test testing over all
    prime basis < b
    """
    basis = [randint(1,n-1) for i in range(b)]
    if n == 2 or n == 3:
        return True

    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    for b in basis:
        x = pow(b, s, n)
        if x == 1 or x == n - 1:
            continue
        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False
    return True

1.2 NTL

因为ntl运行接口较慢且难以拓展，不作为本篇重点。

#include<iostream>
#include<NTL/ZZ.h>

using namespace std;
using namespace NTL;

void Fermat1(ZZ a,ZZ p)
{
	cout << "请输入p：";
	cin >> p;
	a = RandomBnd(p - 1);
	for (int i = 0; i < 5; i++)
	{
		while (GCD(a, p) != 1)
		{
			a = RandomBnd(p - 1);
		}
		
		if (PowerMod(a, p - 1, p) == 1)
		{
			a = RandomBnd(p - 1);
		}
		else
		{
			cout << "p不是素数";
			break;
		}
		if (i == 4)
		{
			cout << "p是素数";
		}
	}
}

void SoSt(ZZ a, ZZ p)
{
	cout << "请输入p：";
	cin >> p;
	while (p > 2 && p % 2 == 0)
	{
		cin >> p;
	}
	a = RandomBnd(p - 1);
	for (int i = 0; i < 5; i++)
	{
		while (GCD(a, p) != 1)
		{
			a = RandomBnd(p - 1);
		}
		if (PowerMod(a, (p - 1) / 2, p) == Jacobi(a, p) || PowerMod(a, (p - 1) / 2, p) == Jacobi(a, p) + p)
		{
			a = RandomBnd(p - 1);
		}
		else
		{
			cout << "p不是素数";
			break;
		}
		if (i == 4)
		{
			cout << "p是素数";
		}
	}
}

int main()
{
	ZZ a, p;
	Fermat1(a, p);
	SoSt(a, p);
}

2. 链接：雅各比符号及其haskell实现

前文我们提到了，雅各比符号是对勒让德符号的一种拓展，那么我们先从勒让德符号讲起。

2.1 勒让德符号

勒让德符号本质上反映了一个非0数是否为另一个素数的二次剩余。

我们知道，一个质数形成的有限域，其域上非零元素一半为二次剩余一半为非二次剩余。

即\[x^2=a \pmod {p}\]有解<==>\[(\frac{a}{p})==1\]。

特性：

积性函数：\[(\frac{ab}{p})=(\frac{a}{p})(\frac{b}{p})\]
\[(\frac{a^2}{p})=1\]
\[(\frac{a}{p})=(\frac{b}{p})\],当\[a\equiv b \pmod {p}\]
$(\frac{p}{q})=(-1)^{\frac{p-1}{2}\cdot\frac{q-1}{2}}(\frac{q}{p})$
$(\frac{-1}{p})=(-1)^{\frac{p-1}{2}},(\frac{1}{p})=1$
$(\frac{2}{p})=(-1)^{\frac{p^2-1}{8}}$

以上性质，说明了这个函数是一个可递归实现的函数：

性质1为递归提供了子问题划分的条件（类似欧拉函数）。

性质4为递归提供了稳态破坏的条件。

性质3为递归提供了子问题的一种等价划分

性质5，6为递归提供了递归的终止态。

2.2 雅各比符号

雅各比符号进一步把素数推广为非偶数的正整数，并继承了以上性质，因此雅各比符号也是可递归实现的，适合使用函数式实现。

需要注意的是，雅各比符号毕竟是使用的非质数m进行推广，其在二次剩余上的意义被打破，对于判断在非有限域下的其他整数环中是否为二次剩余没有指导意义。

除此之外，在1.1.1节中我们提到了雅各比符号与模幂运算之间的内在关联，因此在此我们可以下一个粗浅的结论来解释雅各比符号中加入的值0的含义：

$(\frac{a}{m})==0<=>gcd(m,a)!=1$

2.3 haskell

2.3.1 haskell简介

haskell是目前最为接触数学的编程语言，其纯函数式的特性使得其在大部分数学函数的实现中以无可比拟的美感起到了令人震撼的作用。

2.3.2 haskell jacobi符号实现

jacobi :: (Integral a)=>a->a->a
jacobi n m
  | (m < 0) = error "neg m"
  | (m `mod` 2 == 0)  = error "even m"
  | otherwise = jacobi' n m

jacobi' :: (Integral a)=>a->a->a
jacobi' 1 _ = 1
jacobi' (-1) m = (-1) ^ (div (m-1) 2)
jacobi' 0 _ = 0
jacobi' 2 m = (-1) ^ (div (m^2-1) 8) 
jacobi' n m
  | n < (-1)  = (jacobi' (-1) m ) *(jacobi' (- n) m)
  | n > m = jacobi' (n `mod` m) m
  | (n `mod ` 2 == 0) = (jacobi' 2 m)*(jacobi' (div n 2) m)
  | otherwise = (jacobi' (-1) (div (m*n-m-n+3) 2))*(jacobi' m n)

主函数jacobi主要处理了报错信息，计算函数jacobi'处理了对应的递归模式。

可以看到，jacobi在haskell上的实现代码量最多是相同Python实现的1/2。

3. 数据测试及性能比较

3.1 单轮素数检测

由于在实际计算中，sage的底层引用一般不选择NTL，所以导致其实现较快（还没读源码，猜测问题是出在了对大数的内存管理上），因此本次测试我们统一使用sage。

3.1.1 单轮检测代码1

test_number=[int(i) for i in """
115921 252601 72934879102271241648426492271730744633800277079752665073951 22356556428347371191698399214467787018791948334691697578290577962216876499377539334483720552975347714328452036074010604373528959269622147129120835027063319925220078829082931022948650474024417050974139419013871612480613081473425031484830581421090988945262028469222454196445529288787619959670372054180614638559 59781728296291796158017561748790663563089826605613453665484905474067787844371928298271399443627910058186271964388689059202384502829570397941413694221362295301992777901316834935383384311335512396099609207669093853533128308369361287391546232562965636847929476475654404583285950058456806751391620048033664557683 28494763464967883432404625600246500270772945929877245405931752469865039864230821468097563814857376172612971356800192745072503914472425803446304874347819820876404436537980316277614506865977235566602316683632497367119801578047171561102922761465857684859995527428337609809476794854474027492330502370339054042789
""".split()]
for j in range(10):
	print("round"+str(j))
	for i in test_number:
		print(Fermat(i),Solovay_Strassen(i),miller_rabin(i,1))

输出10轮，结果如下：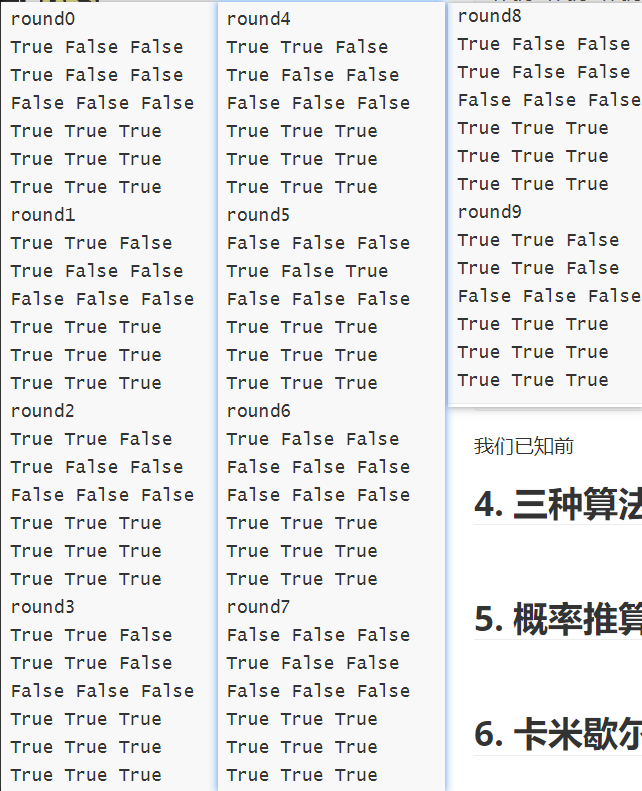

我们已知前三个数为合数，后三个数为质数，可以发现，在质数的情况下，三个算法的输出都完全正确，但在合数的情况下则出现问题，我们定义在本次实验中前三个数判断正确的次数为hit，有：

num	F	S	M
115921	1	5	10
252601	1	8	9
729348……	10	10	10

可以发现单轮miller实现效果较好，基本都成功反映了效果

但对于F和S两个算法，在一部分数上的实现效果较差。

由于这几种算法都是概率化算法，所以我们需要更多数据来测算到底每个算法的概率如何。

3.1.2 单轮检测代码2

dic=[[0,0,0],[0,0,0],[0,0,0]]
for j in range(100000):
    for i in range(3):
        t=[Fermat(test_number[i]),Solovay_Strassen(test_number[i]),Miller_rabin(test_number[i])]
        for k in range(3):
            if t[k]==False:
                dic[i][k]+=1


for i in range(3):
    for j in range(3):
        dic[i][j]/=100000
        dic[i][j]=float(dic[i][j])


print(dic)

输出结果

[[0.10542, 0.55227, 0.96472], [0.04881, 0.52552, 0.92677], [1.0, 1.0, 1.0]]
[[0.10411, 0.55115, 0.96558], [0.04945, 0.52453, 0.92573], [1.0, 1.0, 1.0]]
[[0.10445, 0.55192, 0.96502], [0.05026, 0.52759, 0.92602], [1.0, 1.0, 1.0]]
[[0.10541, 0.55304, 0.9654], [0.05097, 0.52545, 0.92639], [1.0, 1.0, 1.0]]
[[0.1052, 0.55266, 0.96401], [0.04878, 0.52237, 0.9243], [1.0, 1.0, 1.0]]
[[0.10775, 0.55398, 0.96516], [0.04912, 0.52314, 0.92467], [1.0, 1.0, 1.0]]

可以发现以下特征：

对于第三个合数的识别无论算法单轮都达到了100%，而对于前两个素数则有所差异。
可以发现对于前两组数据，每个算法都有自己的趋向值，由于选择次数为10000，且多轮重复可认为较大，所以可得到以下概率表

numrate F S M

115921 10% 55% 96%

252601 5% 52% 92%

729348…… 100% 100% 100%
如果单独对于算法进行分析，费马的概率最低，在10%左右；solovay_Strassen的概率在50%左右，miller的概率接近100%

numrate	F	S	M
115921	10%	55%	96%
252601	5%	52%	92%
729348……	100%	100%	100%

为了进一步探究，我们又选择了三个随机生成的合数[855253, 625886, 865844]进行实验

得到结果

[[0.99996, 0.99996, 0.99998], [1.0, 0.49988, 1.0], [1.0, 1.0, 1.0]]
[[0.99998, 1.0, 1.0], [1.0, 0.5006, 1.0], [1.0, 0.99998, 1.0]]
[[0.99996, 0.99996, 1.0], [1.0, 0.50109, 1.0], [1.0, 0.99999, 1.0]]
[[0.99996, 0.99998, 1.0], [1.0, 0.50033, 1.0], [1.0, 0.99998, 1.0]]
[[0.99993, 0.99998, 0.99999], [1.0, 0.50036, 1.0], [1.0, 0.99999, 1.0]]
[[0.99993, 0.99999, 0.99999], [1.0, 0.49851, 1.0], [1.0, 1.0, 1.0]]

可以发现似乎大部分情况下，费马法和米勒法的结果都是高置信的，而solovay_Strassen的结果不是50%就是接近100%。

那么在这个基础上，我们暂且给出以下结论：

给出的前两组数据，有特殊性，且较为稀少。
对于这类特殊数据，费马法发挥不佳，成功概率姑且认为是10%；对于其他数据成功概率则接近100%
solovay_Strassen算法对于大部分数据，成功概率都在50%或者100%左右，我们保守估计，取50%作为单轮的成功概率；
miller对于特殊数据的成功率也有降低，但不多我们保守估计按照90%作为单轮的成功概率。

3.2 多轮素数检测

我们假设要求成功率高于99.99%，则有$hit\_rate^x<1-99.99\%$,计算得，对于三种算法的测试轮数应为

费马：88

solovay_Strassen ：14

million：4

进行测试

3.2.1 多轮检测代码1

1 2	for i in test_number: print(fermat(i,88),solovay_Strassen(i,14),miller_rabin(i,4))

测试十次，结果均正确。（不再放图）

3.2.2 多轮检测代码2

源代码

dic=[[0,0,0],[0,0,0],[0,0,0]]
for j in range(100000):
    for i in range(3):
        t=[Fermat(test_number[i]),Solovay_Strassen(test_number[i]),Miller_rabin(test_number[i])]
        for k in range(3):
            if t[k]==False:
                dic[i][k]+=1


for i in range(3):
    for j in range(3):
        dic[i][j]/=100000
        dic[i][j]=float(dic[i][j])

print(dic)

输出结果

[[0.99994, 0.99998, 0.99999], [0.98911, 0.99995, 0.99999], [1.0, 1.0, 1.0]]
[[0.99991, 0.99999, 1.0], [0.98901, 0.99995, 0.99995], [1.0, 1.0, 1.0]]
[[0.99992, 1.0, 1.0], [0.98869, 0.99999, 0.99998], [1.0, 1.0, 1.0]]
[[0.99998, 0.99999, 1.0], [0.98911, 0.99998, 0.99996], [1.0, 1.0, 1.0]]

发现对于第二组，费马成功率不达标，原因是他的单轮成功率为5%左右，而不是我们预期的10%。

代入计算得 $1-0.95^{88}=0.989$,符合实际效果。那么对于本数据，若达到99.99%置信度，实际次数应为180，对其单独测试，有输出：

1	0.99985，0.99984，0.99993，0.99991，0.9999

基本符合预期。

4. 三种算法的原理再探究

从刚刚的数据测试以及性能比较中我们发现两个问题：

1.算法是概率的；

2.算法稳定性是随具体数据而变化的。

在实际应用中显然我们不能先测出来具体数据的成功概率再进行校验，但如果能找到一个确定的上界，我们就可以按照这个上界把单轮变为多轮来进行测算。因此，我们需要了解算法的具体细节，进行原理再探究。

4.1 “凭证”

对于待测数p,若有任意正整数a,若a使得对应算法判断p为合数，则称a为p的一个凭证；否则则为一个强伪证。

4.2 solovay_Strassen算法

通过查阅资料得知，该算法的凭证约有二分之一，与我们的估计相同，具体证明未见。

4.3 miller_rabin算法

根据《算法数论》等资料，我们知道miller_rabin的凭证约有1/4，具体证明参见Rabin在1977年的论文中证明了下列定理：若$n$为大约4的合数，则有

\[\frac{3(n-1)}{4} \leq c({b | W_n(b)})\]

其中$W_n(b)$表示$b$是$n$为合数的一个凭证；$c(S)$表示集合$S$中元素的数目。上述定理表明，在$[1, n-1]$的整数中，最多只有$\frac{1}{4}(n-1)$个数不是$n$为合数的凭证。因此，在$[1, n-1]$中任选整数$a$进行测试，能够测试出$n$为合数的概率$\leq \frac{3}{4}$，即Miller-Rabin算法的错误概率不大于$\frac{1}{4}$。

然而，这个数据与我们测试的并不相符，事实上，他还有更紧的界，证明如下：

如果我们不断随机选取$k$位（二进制位）的奇数，对这个数进行$t$次互相独立的随机Miller-Rabin检测，输出第一个通过所有测试的数，令$p_{k, t}$表示这个数是合数的概率，则$p_{k, t}$比$4^{-t}$小得多。事实上，$p_{k, t}$满足下列公式：

$k \geq 2$时，$p_{k, t} < k^2 4^{2 - \sqrt{k}}$

$t = 2, k \geq 88$或$3 \leq t \leq k/9, k \geq21$时，$p_{k, t} < k^{3/2} 2^t t^{-1/2} 4^{2 -\sqrt{tk}}$

$t \geq k/9, k \geq 21$时，$p_{k, t} < \frac{7}{20} k 2^{-5t} + \frac{1}{7} k^{15/4} 2^{-k/2 - 2t} + 12k 2^{-k/4 - 3t}$

$t \geq k/4, k \geq 21$时，$p_{k, t} < \frac{1}{7} k^{15/4} 2^{-k/2 -2t}$

4.4 费马小定理

通过资料我们得知，费马小定理的凭证一般而言约有1/2，具体证明如下：

对于$n=p_1^{m_1}p_2^{m_2}p_3^{m_3}\cdots$,则有$n-\phi{(n)}$个数与之不互素，这些数的非0次模幂组成的群本身就不包含1这个元，所以有至少$m=n-1-\phi{(n)}$个数是凭证，对于非这m个数的数，我们认为其为潜在的凭证。

若其中有一个数a为凭证，则对于某个潜在凭证b，若b不为凭证，则$(a*b)^{n-1}=a^{n-1}*1\neq 1 \pmod n$，即a*b也是凭证，我们取所有不等的潜在凭证中的非凭证为$\{b_k\}$，则对于a产生均可以产生$c_k=ab_k$的凭证，这时我们可以知道对于$i\neq j$，$c_i\neq c_j$（否则可以乘a的逆元得到$b_i=b_j$，与题设矛盾）于是这2k个数形成m个数的一个子集，可知非凭证数小于$\frac{\phi(n)}{2}$，即还有至少$\frac{\phi(n)}{2}$个数为凭证，这时凭证数$w>\frac{n}{2}$。

但是其中如果一个凭证都没有的时候呢？这个问题我们留到第六节细细讨论。

我们首先回归本章最初提出的问题：如何选择实际运行的参数？

5. 概率推算与参数选择

假设要求成功率高于99.99%，则有$hit\_rate^x<1-99.99\%$。计算得，对于三种算法的测试轮数应为：

solovay_Strassen与fermat算法大致需要14次；

miller_rabin算法需要7次。

而另一方面我们又知道，这个参数的选择与具体数据有关，通过查阅工业界资料，我们发现数据的长度也对选择次数有一定影响，以OpenSSL为例，我们可以发现如下表格：

除此之外，在工业界中我们发现一般只使用miller_rabin算法和其他准确定性算法以及基于连分数或数列的概率算法。

使用这些参数再去分析算法，我们发现对于最开始的两组测试数据依旧无法解释他们的反常，而通过四五节的分析，我们有理由怀疑这并不是算法的错误，而是数据本身具有特殊性质，即满足4.4中提到的，”没有非平凡凭证的数“。

6. 寻找特殊数

6.1 卡米歇尔数

卡迈克尔数的定义是对于合数n，如果对于所有与n互质的正整数b，都有同余式b^(n-1)≡ 1 (mod n)成立，则称合数n为Carmichael数。

卡米歇尔数有一些特殊性质：

每个Carmichael至少是三个不同素数的乘积。
对于每个Carmichael p，对于任意非零整数a，有$a^{p}≡ a (mod p)$。即，卡米歇尔数满足费马小定理。

这充分说明了，满足费马小定理并不是素数的充要条件，他只是一个必要性条件，但不充分。事实上，当前社会条件下，我们仍未找到被完全证明的，可计算性良好的与素数等价的条件，这也是素数这么神奇的一个原因。

6.2 伪素数

既然素数并没有等价的充要条件，那么我们能不能推广定义出相对于其他必要性的”伪素数“呢？

通过查阅资料我们发现，这种推广定义确实存在，而且的确被应用于工业界并造成了问题。

7. 实际使用中的一些“优化”

7.1 工业问题

在实际工业产品中，我们会注意发现这样一些问题：

相比与素数，合数成为凭证的难度更大，带来的判断效果整体上不如素数更专一；
实际检测数据长度不定带来产生随机数的数据范围不定，在更大的范围中，随机数算法会失效，或其随机效果打折扣；
使用更大的数据来判断时，会耗费更多资源，同时减慢速度，而较小的一些常用素数就已经可以应对在一定范围内的所有数据的正确性。

7.2 工业优化

在实际工业中，使用的miller_rabin算法往往会有以下的“优化”方案：

使用一个限定小范围内的随机数进行判断以降低运算量
减少判断次数以提高速度
使用固定基进行判断

那么针对以上这些速度优化带来的算法漏洞，我们有没有什么可以进行绕过呢。

答：必然存在，以下就是一个经典的例子。

8. 素性检测带来的经典漏洞：CVE-2018-4398

CVE-2018-4398 是发生于苹果设备上的一个通用漏洞，产生原因是在miller_rabin算法中使用了固定的一组素数基。具体细节可参考《prime and prejudice》

文中提到了一种关于这类素数检测攻击方式，来源是95年的论文《Fran¸cois Arnault. Constructing Carmichael numbers which are strong pseudoprimes to several bases. Journal of Symbolic Computation》，接下来我们来复现一下。

1. 强伪证定理

文中提到了这样一个定理：对于$n=p_1p_2p_3\cdots$,给定参数$k_i=\frac{p_i-1}{p_1-1}$,$m_i=\frac{\Pi_{i\neq j}(p_i-1)}{p_i-1}$,如果$k_i$为奇整数，$m_i$为整数，且对于检测基b,均有$(\frac{b}{p_i})=-1$,则b是n的强伪证。

2. 证明

由于$k_i$为整数，则$b^{(n-1)/2}=b^{(2m+1)(p_i-1)/2}=(b^{(p_i-1)/2})^{2m+1}=(b^{(p_i-1)/2})=(\frac{b}{p_i}) \pmod n$,

因此当$(\frac{b}{p_i})=-1$，若有取$S_b\subset\mathbb{Z}/4b\mathbb{Z}$,则有$p 4b S_b $,那么$p_i=k_i(p_1-1)+1 4b S_b$，则如果$gcd(k_i,b)$，$p_1 4b k^{-1}_i(S_b-1+k_i)$，因此可知对于每一个质数，该集合中的数均满足强伪证，原式得证。

3. 漏洞复现

由于我们并不能看到apple的原始基是什么，但我们找到了这个漏洞的复现题目Cryptohack

基本思路就是按照以上定理暴力，依次试出解素数的解，剩下的就是crt构造伪质数。

4. 题目脚本

由于Cryptohack的规矩，题解不能公开，所以仅放部分核心代码如下

for p in primes:
    f = set()
    for i in generate_basis(200*p)[1:]:
        if legendre(p, i) == i-1:
            f.add(i % (4*p))
    fool.append(list(f))
    
fool2 = []
for p, f in enumerate(fool):
    prime = primes[p]
    m = prime*4
    cur_set = set(f)
    for i in range (1, h):
        new_set = set()
        for ff in f:
            if ((ff + ks[i] - 1)*inverse(ks[i], m)) % 4 == 3:
                new_set.add(((ff + ks[i] - 1)*inverse(ks[i], m)) % m)
        cur_set = cur_set.intersection(new_set)
    fool2.append(cur_set)

9. 一些感想

其实写这篇实验报告是因为做到了这个题目，正好遇到这次实验，所以又去深究了一番。

搜索资料不免会看到余建春，于是想想别人在那么一个非学术甚至非学术友好的环境里做出了为学界所称赞的成就，想起自己在一个如此鼓励学术的环境中占用着那么多资源，却迟迟做不出像样的贡献，浪费着纳税人的钱与师长们的期望，心里总会惴惴。偶尔也想做一些划水的事，或者做一些金玉其外败絮其中的面子事，但总觉得无以面见在天之灵，举头三尺的地方总有大家与大众不可辜负。于是回想起生存道路，走到现在的每一步都离不开其他人的帮助，这条命所得所失都不是我个人的，所以写的东西做的事都不敢懈怠，做，就做到至少让自己挑不动刺，拿出实打实的东西，而不是花拳绣腿重形式轻内容。毕竟，你我逢场作戏随意丢弃的，都有可能是其他人一生求之不得的东西。

认识一些朋友，很有学密码的灵性，在自己的摸索下走到了我们望尘莫及的地步，我常常想，如果在山大的不是我而是他，有着更好的师资，是不是能做出更大的成就。每每想到这里，就觉得自己还是不能放弃这些难走的路，毕竟人家也曾经理解我认同我支持我，期待着我能做些什么，人不能为了自己那一点前路通畅而无视他人的期望，这一点知遇之恩，来之不易，并非理所当然。

10.参考资料

Fermat素性检测算法（为什么每次概率改变1/2）

Miller-Rabin素性检测的原理与实现

费马见证

Cryptohack

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。