AES与SM4
聊聊AES与SM4。
算法细节
基本比较
| 算法名称 | 密钥长度 | 分组长度 | 循环次数 | 算法结构 |
|---|---|---|---|---|
| AES | 128/192/256 | 128 | 10/12/14 | Substitution-Permutation |
| SM4 | 128 | 128 | 32 | 非平衡Feistel |
(注:AES常用密钥长度128,轮数10)
操作对比
AES每轮的操作包括(1)Sbox变换(2)行移位(3)列混淆【除最后一轮】(4)密钥轮加。
SM4每轮的操作包括(1)密钥轮加(2)Sbox变换(3)基于移位的线性变换。
重点区别:轮密钥加密的位置。
密钥调度
AES使用了10个系统参数,但生成过程分情况讨论产生,较为繁琐。
SM4使用了4个系统参数和32个轮拓展参数,生成过程中使用了简单的异或算法。
加解密流程
AES加解密算法不同,轮密钥倒置。
SM4加解密算法相同,轮密钥倒置。
魔数
AES轮拓展参数:RC[11]={0x00,0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1B,0x36};
SM4轮拓展参数: FK[4]={0xa3b1bac6,0x56aa3350,0x677d9197,0xb27022dc};
CK[32]={
0x00070e15,0x1c232a31,0x383f464d,0x545b6269,
0x70777e85,0x8c939aa1,0xa8afb6bd,0xc4cbd2d9,
0xe0e7eef5,0xfc030a11,0x181f262d,0x343b4249,
0x50575e65,0x6c737a81,0x888f969d,0xa4abb2b9,
0xc0c7ced5,0xdce3eaf1,0xf8ff060d,0x141b2229,
0x30373e45,0x4c535a61,0x686f767d,0x848b9299,
0xa0a7aeb5,0xbcc3cad1,0xd8dfe6ed,0xf4fb0209,
0x10171e25,0x2c333a41,0x484f565d,0x646b7279};
(注:将CK拆解为char数组ck[128],则ck[i]=7*i mod 256)
Sbox
AES
Sbox={
0x28,0xC2,0xE8,0x57,0x48,0x24,0x97,0xC5,0x18,0x8C,0x9B,0x72,0xF7,0x99,0xDE,0xD3,
0x85,0x58,0x7A,0x0B,0x44,0xD1,0xB0,0x47,0xC7,0xAE,0xF0,0x6D,0x53,0xE1,0x60,0xB4,
0x4B,0x5C,0x10,0x52,0x01,0x39,0xB9,0x90,0xAB,0x00,0xD4,0x73,0x64,0x32,0x9F,0xA1,
0x6A,0x1C,0x6B,0x21,0xF1,0xEF,0x3F,0x67,0x95,0xF2,0x79,0xE0,0x0C,0xD0,0x66,0x7F,
0x2C,0xC3,0x12,0x5A,0x34,0xEB,0x15,0xA6,0xBC,0x7D,0xA0,0xB8,0x55,0x49,0xC1,0xFB,
0xE9,0x08,0x3C,0xE2,0x56,0x2F,0x30,0x9E,0x0E,0xCB,0x25,0xE3,0x46,0x5D,0xEC,0x4C,
0x09,0xBE,0x87,0x04,0x89,0xD8,0x19,0x3D,0x71,0x40,0x7E,0x5F,0x16,0x7B,0x3A,0x27,
0x43,0x76,0x45,0x8A,0x35,0x96,0xF9,0x07,0x8F,0x0F,0x54,0xCF,0xBA,0x38,0x83,0xCE,
0x2A,0xAC,0x68,0xF4,0x80,0x31,0xA4,0xFE,0x93,0xB3,0x7C,0xCA,0xB6,0x75,0xDA,0xA8,
0xD7,0xB1,0x37,0xC4,0x6C,0x6F,0xD5,0x4F,0x23,0x14,0x98,0xAA,0xDC,0x65,0x74,0x42,
0xC8,0x41,0x8D,0xA5,0x22,0xEA,0x4D,0xB5,0x17,0x02,0x1E,0x88,0x91,0x33,0xC6,0x78,
0x3B,0x2D,0xD9,0xFC,0x1B,0x9A,0xCD,0xE6,0x1F,0xED,0x92,0x29,0x4A,0xFA,0x1A,0xEE,
0x0D,0xE7,0x63,0x8E,0xFF,0x06,0x3E,0x1D,0xF8,0xAD,0xE5,0x36,0x05,0x70,0xA2,0x69,
0x84,0xBF,0xA9,0x8B,0x03,0xD6,0x26,0x2E,0x82,0x62,0x81,0xE4,0x94,0xA7,0xAF,0x5E,
0x9D,0xD2,0xB2,0x86,0x2B,0x51,0xCC,0xDD,0x13,0xF5,0x77,0x50,0xC0,0xB7,0x0A,0x59,
0x4E,0xC9,0xBB,0x11,0xA3,0x6E,0xDB,0xF6,0x61,0x9C,0x20,0xDF,0xFD,0xBD,0x5B,0xF3}
SM4
Sbox={ 0xd6,0x90,0xe9,0xfe,0xcc,0xe1,0x3d,0xb7,0x16,0xb6,0x14,0xc2,0x28,0xfb,0x2c,0x05,
0x2b,0x67,0x9a,0x76,0x2a,0xbe,0x04,0xc3,0xaa,0x44,0x13,0x26,0x49,0x86,0x06,0x99,
0x9c,0x42,0x50,0xf4,0x91,0xef,0x98,0x7a,0x33,0x54,0x0b,0x43,0xed,0xcf,0xac,0x62,
0xe4,0xb3,0x1c,0xa9,0xc9,0x08,0xe8,0x95,0x80,0xdf,0x94,0xfa,0x75,0x8f,0x3f,0xa6,
0x47,0x07,0xa7,0xfc,0xf3,0x73,0x17,0xba,0x83,0x59,0x3c,0x19,0xe6,0x85,0x4f,0xa8,
0x68,0x6b,0x81,0xb2,0x71,0x64,0xda,0x8b,0xf8,0xeb,0x0f,0x4b,0x70,0x56,0x9d,0x35,
0x1e,0x24,0x0e,0x5e,0x63,0x58,0xd1,0xa2,0x25,0x22,0x7c,0x3b,0x01,0x21,0x78,0x87,
0xd4,0x00,0x46,0x57,0x9f,0xd3,0x27,0x52,0x4c,0x36,0x02,0xe7,0xa0,0xc4,0xc8,0x9e,
0xea,0xbf,0x8a,0xd2,0x40,0xc7,0x38,0xb5,0xa3,0xf7,0xf2,0xce,0xf9,0x61,0x15,0xa1,
0xe0,0xae,0x5d,0xa4,0x9b,0x34,0x1a,0x55,0xad,0x93,0x32,0x30,0xf5,0x8c,0xb1,0xe3,
0x1d,0xf6,0xe2,0x2e,0x82,0x66,0xca,0x60,0xc0,0x29,0x23,0xab,0x0d,0x53,0x4e,0x6f,
0xd5,0xdb,0x37,0x45,0xde,0xfd,0x8e,0x2f,0x03,0xff,0x6a,0x72,0x6d,0x6c,0x5b,0x51,
0x8d,0x1b,0xaf,0x92,0xbb,0xdd,0xbc,0x7f,0x11,0xd9,0x5c,0x41,0x1f,0x10,0x5a,0xd8,
0x0a,0xc1,0x31,0x88,0xa5,0xcd,0x7b,0xbd,0x2d,0x74,0xd0,0x12,0xb8,0xe5,0xb4,0xb0,
0x89,0x69,0x97,0x4a,0x0c,0x96,0x77,0x7e,0x65,0xb9,0xf1,0x09,0xc5,0x6e,0xc6,0x84,
0x18,0xf0,0x7d,0xec,0x3a,0xdc,0x4d,0x20,0x79,0xee,0x5f,0x3e,0xd7,0xcb,0x39,0x48}
SBox的数学原理
Sbox几乎是对称密码里共有的唯一非线性元件,对加密的安全性定义起到核心作用。
多项式
抽出具体运算对象,用未定元占位进行运算。
加法:同类项合并/不进位加法 -----》(构成群)
乘法:柯西乘积 --------》(构成环)
数乘:退化到度为0的乘法 ------》(向量空间)
除法:带余除法 -------》(有限域)
\[GF(2^8)\]
在多项式运算的基础上,将数域选为整数,引入2将每个系数限定在{0,1}域内,再引入一个8次不可约多项式作为模元得到\(GF{(2^8)}\)。
求模运算:若
一些有趣的性质:
- 加法与加法逆元是相同的。
- 数乘进一步退化为保持或归零两种操作,可部署进电路。
- 不可约多项式作为模元,域内每一个元素都可以作为原根。
多项式基与正规基
多项式基是\(\{x^{n-1},\cdots,x,1\}\),其中x为占位未定元。
取A=0b10,则\(GF(2^8)\)的多项式基即为\(\{A^7,A^6,A^5,A^4,A^3,A^2,A^1,1\}\)
性质
- 加法及逆元等价于按位异或。
- 单项式乘法等价于移位。
- 对于乘方运算实现较为困难。
正规基\(\{Y^{p^{n-1}},\cdots,Y^{p^1},Y\}\),其中p是GF(p)所对应的阶数。
性质
- \(Y^{p^{n}-1}=1,Y^{p^n}=Y\)。
- 正规基使用了多项式的全部根,不含有元素1
- 扩域上乘方运算等价于换位。
- 乘法运算较为方便。
Sbox的构造
AES和SM4的构造虽然有较大的具体差异,但都是线性运算和求逆运算的结合,其中求逆运算是核心功能。
求逆可以转化为在对应域上的幂运算,但直接在\(GF(2^8)\)上的运算很麻烦,而另一方面,二次扩域的求逆较为简单,所以我们可以把他转化为多个二次扩域的复合进行计算。
域复合
在\(GF(p^n)\)的空间里寻求一个gcd(r,n)!=1,使得\(GF(p^r)\)是原空间的一个子空间,则按照子空间进行划分,我们就能划分出商空间\(GF(p^n/p^r)\)使得\(x^r\)为最小未定元单位。
使用分治,我们可以通过两次划分获得\(GF(2^8)\)与\(GF(2^2)\)产生同构,即\(GF(2^8/2^4),GF(2^4/2^2)\),在这几组子域的二次扩域均为两组基。
求逆
由于求逆主要涉及幂运算,在正规基下乘法运算特别是幂运算更加方便,所以取正规基下的求逆过程。
模元r我们可以表示为\(r(y)=y^2+by+c=(y+Y^{p^r})(y+Y)\),即\(b=Y^{p^r}+Y\), \(c=Y^{p^r}\cdot Y\)
我们可以取任意元素g,使得\(g={g_1Y^{p^r}+g_0Y}\),那么其逆元\(d={d_1Y^{p^r}+d_0Y}\)满足
\(gd=g_1d_1(Y^{p^r})^2+(g_1d_0+g_0d_1)Y^{p^r}Y+d_0d_1Y^2\)
\(=g_1d_1(bY^{p^r}+c)+(g_1d_0+g_0d_1)c+g_0d_0(bY+c)\)
\(=(g_1d_1bY^{p^r}+g_0d_0bY)+[g_1d_1c+(g_1d_0+g_0d_1)c+g_0d_0c]\)
\(=(g_1d_1bY^{p^r}+g_0d_0bY)+[(g_1+g_0)(d_1+d_0)c]b^{-1}(Y^{p^r}+Y)\)
\(=[g_1d_1b+(g_1+g_0)(d_1+d_0)cb^{-1}]Y^{p^r}+[g_0d_0b+(g_1+g_0)(d_1+d_0)cb^{-1}]Y)\)
=1 \(=b^{-1}(Y^{p^r}+Y)\)
得
\(b^{-1}=g_1d_1b+(g_1+g_0)(d_1+d_0)cb^{-1}\)
\(b^{-1}=g_0d_0b+(g_1+g_0)(d_1+d_0)cb^{-1}\)
相加有
\(g_0d_0+g_1d_1=0\),即\(g_0d_0=g_1d_1\)
乘b得
\(1=b^2g_0d_0+(g_1d_0+g_0d_1)c\)
乘\(g_1\)得
\(g_1=g_0g_1d_0b^2+(g_1^2d_0+g_0g_1d_1)c\)
\(=g_0g_1d_0b^2+(g_1^2d_0+g_0^2d_0)c\)
\(=[g_0g_1b^2+(g_1^2+g_0^2)c]d_0\)
即
\(d_0=[g_0g_1b^2+(g_1^2+g_0^2)c]^{-1}g_1\)
\(d_1=[g_0g_1b^2+(g_1^2+g_0^2)c]^{-1}g_0\)
至此便求出了逆元的表达式。
而在\(GF(2^2 )\)上
r(y)有且仅有\(r(y)=y^2+y+1\),即b=c=1
在这里有\(g_i^n=g_i\)
则
\(d_0=[g_0g_1+(g_1^2+g_0^2)]^{-1}g_1\)
\(=[g_0g_1+(g_1^2+g_0^2)]g_1\)
\(=g_0g_1^2+g_1^3+g_0^2g_1\)
\(=g_0g_1+g_1+g_0g_1\)
\(=g_1\)
同理
\(d_1=g_0\)
这样就完成了递归求逆。
基变换
在应用中,b常取1,C取前一组基。
通过三次扩域计算根据模元将原式转换为3个两组基,再对应相乘即可得到八组基,与原式一一对应。
即
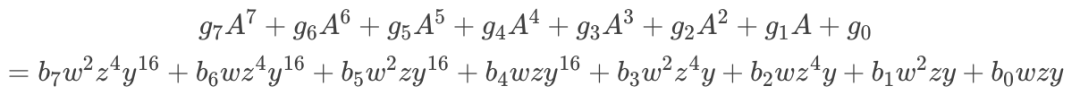
通过以上过程求出y,z,w三组基变换矩阵和逆变换矩阵。与对应的矩阵乘起来即可。
一些结论
对于AES:
- 其生成表达式为\(S_{AES}(x)=Ax^{-1}+0x63\)

- 多项式基在复合域下的表示如下:

- 复合域基在多项式基下的表示如下:

对于SM4:
生成表达式为:\(S_{SM4}(x)=A(Ax+c)^{-1}+c, c=0xd3\)

多项式基在复合域下的表示如下:

- 复合域基下多项式基的表示如下: \[ \left( \begin{matrix} b_7\\b_6\\b_5\\b_4\\b_3\\b_2\\b_1\\b_0 \end{matrix} \right) =\left( \begin{matrix} 0&1&1&0&1&1&1&1\\ 0&1&0&1&0&0&0&1\\ 1&0&0&0&0&1&1&1\\ 0&1&0&0&0&1&1&1\\ 0&0&0&1&1&1&0&1\\ 0&0&0&0&0&0&0&1\\ 0&1&0&1&1&0&0&1\\ 1&1&1&0&0&1&0&1 \end{matrix} \right) \cdot\left( \begin{matrix} g_7\\g_6\\g_5\\g_4\\g_3\\g_2\\g_1\\g_0 \end{matrix} \right) \]
S盒的相互转换
我们已知
\(S_a(x)=A_ax^{-1}+C_a\)
\(S_s(x)=A_s(A_sx+C_s)^{-1}+C_s\)
又知在正规基下,求逆的算法是一致的,我们取求逆运算为\(f_n(x)\),其中n代表正规基下的运算。
我们用\(P_a,P_s\)分别指代AES和SM4的正规基转多项式基的基变换矩阵。
则有
\(A_a^{-1}(S_a(x)+C_a)=x^{-1}=P_af_n(P_a^{-1}x)\)
用\(P_ax\)代入x得
\(f_n(x)=P_a^{-1}A_a^{-1}(S_a(P_ax)+C_a)=P_a^{-1}A_a^{-1}S_a(P_ax)+P_a^{-1}A_a^{-1}C_a\)
而
\(S_s(x)=A_sP_sf_n(P_s^{-1}(A_sx+C_s))+C_s\)
\(=A_sP_sP_a^{-1}A_a^{-1}S_a(P_aP_s^{-1}(A_sx+C_s))+A_sP_sP_a^{-1}A_a^{-1}C_a+C_s\)
取\(Ss(x)=L(Sa(Mx+T))+C\)
则有 \[ \left\{ \begin{array}{llll} L=A_sP_sP_a^{-1}A_a^{-1} \\ M=P_aP_s^{-1}A_s\\ T=P_aP_s^{-1}C_s\\ C=A_sP_sP_a^{-1}A_a^{-1}C_a+C_s \end{array} \right. \] 即
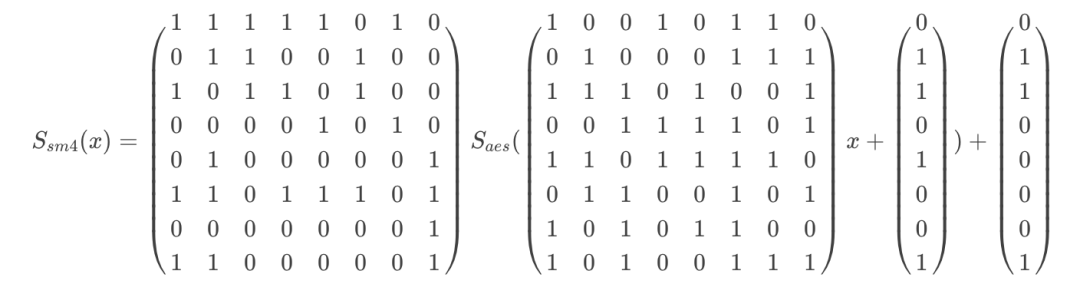
如上,便可在支持AES的芯片内运行SM4的S盒。
